
JavaScript 알고리즘 구현 정리[1]
자바스크립트로 구현한 스택/큐/DFS/BFS 알고리즘을 정리한 게시물이에요. 기존에 개발한 슬랙봇 - AlgoBot에 해당 게시물 주소를 연결하여 정보를 제공할 예정이에요.
목차
- 스택과 큐
- DFS / BFS
스택과 큐
스택과 큐는 쉽게 설명하면 쌓여있는 것이 어떤 순서로 빠져나가는지의 차이라고 생각하면 이해하기 쉬워요.
스택
책상을 정리하기 위해 잠시 책을 하나씩 쌓는 경우를 예시로 들어볼게요. 나중에 이 책을 뺄 때 맨 위에있는 것부터 치우잖아요? 이것이 스택이에요. 마지막에 쌓아 올린 것이 가장 먼저 빠져나가는 후입선출(Last In First Out, LIFO) 형태의 자료구조입니다.
구현은 어렵지 않아요. 단순하게 Array에 push하고 pop하며 빼는 구조를 스택이에요.
Code Example
class Stack {
constructor() {
this.stack = [];
}
push(element) {
this.stack.push(element); // element를 push한다.
}
pop() {
if (this.stack.length === 0) return false // 0인경우 pop 하는 것은 불가능해요.
return this.stack.pop(); // pop한 값을 뺀다.
}
}큐
큐는 스택과 달리 **선입선출(First In First Out, FIFO)**형태의 자료구조입니다. 가게 웨이팅 처럼 먼저 예약을 걸어둔 사람이 먼저 예약 대기열에서 빠져나가는 것으로 생각하시면 이해하기 쉬워요.
주로 배열 형태로 구현하는 경우가 많은데요, Map & 투포인터 형태로 구현할 수 있으니 아래의 예시코드에서 확인해보세요.
Code Example - Array
class Queue {
constructor() {
this.queue = [];
}
push(element) {
this.queue.push(element)
}
popleft() {
// 선입선출의 구조이기 때문에 array 앞부분이 우선적으로 나와야겠죠?
if (this.queue.length === 0) return false
return this.queue.shift();
}
}Code Example - Map
해당 코드는 Map을 생성하고, 맨 앞과 맨 뒤의 인덱스를 조절하면서 구현한 큐에요. 해시테이블 자료구조를 활용하기 때문에 시간복잡도 측면에서 이점이 있지만, 메모리 사용량을 많이 요구하기에 공간복잡도 측면에서는 좋지 못한 알고리즘 구현 방식이에요.
class Queue {
constructor() {
this.queue = new Map();
this.front = 0;
this.back = 0;
}
push(element) {
this.queue.set(this.back++, element);
}
popleft() {
if (this.front === this.back) return false; // 비어있음
const value = this.queue.get(this.front); // 우선 맨 앞의 값을 빼고
this.queue.delete(this.front++); // 맨 앞 인덱스를 조절한 이후 리턴
return value;
}
}DFS / BFS
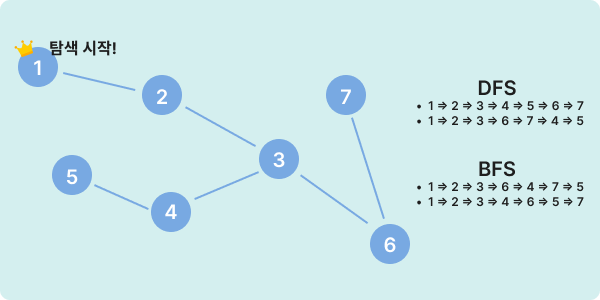
두둥~ 알고리즘 뉴비 절단기 DFS와 BFS입니다. 처음 마주했을 때, 당황스러웠던 기억이 아직도 생생해요. DFS와 BFS의 S는 Search의 약자로 탐색 방식에 관련된 알고리즘이에요. DFS는 Depth-First (깊이 우선), BFS는 Breadth-First (너비 우선) 탐색 방식이에요. 위의 사진에서 명시된 순서가 어째서 저런 순서로 탐색을 진행하는지 아래 예시코드를 통해 알아봐요.
위 노드 그래프는 다음의 관계를 가진다고 가정할게요.
그래프 예시
// key : 해당 노드, value : 해당 노드와 연결된 노드 배열
const graph = {
1: [2],
2: [1, 3],
3: [2, 4, 6],
4: [3, 5],
5: [4], //
6: [3, 7],
7: [6]
};DFS(Depth-First Search)
DFS는 이름 그대로 끝까지 들어가보는 탐색방식입니다. 일단 끝까지 가보고, 더이상 탐색할 수 없다면 탐색해온 경로를 다시 되돌아가 탐색하지 않았던 길을 탐색합니다.
위 예시사진에서 갈림길 3번 노드를 중심적으로 확인해봐요. 3번 노드와 2번 4번 6번 노드가 연결되어 있는데, 이를 이전에 방문한 적 있는지 확인해요. 2번노드, 4번노드, 6번노드를 순차적으로 확인하는 과정에서 4번노드가 방문한 기록이 없음이 확인되면, 그 이후의 확인과정은 진행하지 않고 4번 노드로 탐색을 진행해요.
이후 5번 노드까지 탐색을 진행하면, 탐색할 노드가 더이상 존재하지 않으니 다시 방문했던 노드를 되돌아가며 탐색하지 않았던 노드는 없는지 다시 확인하는 과정을 거쳐요.
그 과정을 통해 3번노드로 되돌아온 경우 6번노드를 아직 탐색하지 않았음을 확인하고 6번노드로 탐색을 진행해요. 이런 방식으로 탐색을 진행하는 방식을 DFS라고 합니다.
Code Example - DFS
function dfs() {
const stack = [];
const visited = new Set(); // 방문 여부를 판단하기 위함
let current = 1;
const trace = []; // 실시간 위치 추적 (어떤 순서로 노드를 확인하는가)
const result = [1]; // 실질적 탐색 노드 순서 (어떤 순서로 노드를 탐색하는가)
stack.push(current);
visited.add(current);
while (stack.length !== 0) {
trace.push(current);
const nextCandidates = graph[current];
let moved = false; // 이동했는지 체크할 플래그
for (const nextCandidate of nextCandidates) {
if (!visited.has(nextCandidate)) {
visited.add(nextCandidate);
stack.push(current); // 현재 노드를 다시 스택에 저장 (되돌아오기 위해)
current = nextCandidate; // 다음으로 이동
moved = true; // 이동했음
result.push(nextCandidate);
break; // 이동했으니까 더 이상 후보 안 본다
}
}
if (!moved) {
// 이동을 못했으면
current = stack.pop(); // 스택에서 이전 경로로 backtrack
}
}
return {
result,
trace,
}
}
console.log(dfs()); // result : [1, 2, 3, 4, 5, 6, 7], trace :[1, 2, 3, 4, 5, 4, 3, 6, 7, 6, 3, 2, 1] (stack이 비면 탐색 종료)BFS(Breadth-First Search)
BFS는 주변을 살피며 탐색하는 방식이라고 생각하면 이해하기 쉬워요. 탐색 가능한 노드를 확인하고 탐색 가능하다면 그 방향으로 쭉쭉 들어가며 탐색했던 DFS와 달리 BFS는 주변에 갈 수 있는 모든 노드들을 확인하면서 탐색을 진행해요.
갈림길이 존재하는 3번 부터 설명해볼게요. 3번에서 4번 노드를 확인한 순간 해당 노드로 탐색을 진행한 DFS와 달리 탐색할 목록 큐에 4번노드와 6번 노드를 모두 저장해둬요. 이 과정까지의 큐는 [4,6] 이에요.
그리고 해당 목록을 보고 4번 노드를 탐색해요. 이후 4번노드에선 또 5번 노드를 탐색할 목록 큐에 저장해요. 이 때 큐를 확인하면 [6, 5]가 되어요.
이후엔 6번 노드를 탐색하고 7번 노드를 큐에 저장해요. 이 땐 [5, 7] 형태의 큐에요.
이런 방식으로 내가 지금 탐색하고 있는 노드의 주변을 확인하고 저장해둔 이후, 해당 노드를 탐색하는 과정의 반복이 BFS라고 생각하시면 이해하기 쉬워요.
Code Example - BFS
function bfs() {
const queue = []; // 다음 탐색할 노드 후보를 담을 큐
const visited = new Set(); // 방문한 노드를 기록
const result = []; // 방문 순서 기록
let current = 1;
queue.push(current);
visited.add(current);
while (queue.length !== 0) {
current = queue.shift(); // 가장 먼저 큐에 들어온 노드를 꺼냄
result.push(current);
const nextCandidates = graph[current];
for (const nextCandidate of nextCandidates) {
if (!visited.has(nextCandidate)) {
visited.add(nextCandidate);
queue.push(nextCandidate);
}
}
}
return result;
}
console.log(bfs()); // [1, 2, 3, 4, 6, 5, 7]DFS, BFS의 사용처
DFS와 BFS모두 길찾기 등의 경로를 찾는 과정에 많이 사용해요. 하지만 큰 차이점은 모든 경로를 고려해야하는 경우 DFS를 사용하는 경우가 많고, BFS는 최단거리나 한칸한칸 퍼져나가는 알고리즘 문제와 같은 경우에 사용해요.
참고로 위에 있는 예시코드를 암기만 한다면 실제 문제에 적용할 수 없어요. 실제 DFS와 같은 경우 재귀함수를 활용하여 구현하는 경우도 많고, 노드간의 관계가 아닌 이차원 배열에서 이를 구현해야하는 경우도 있어요. 또, 조건문을 사용해서 적절하게 끊어주지 않는다면 시간초과, Stack Overflow가 발생하는 경우도 있기에 많은 문제를 풀어보며 감각을 익히는게 중요해요.
트리, 연결리스트, 정렬 알고리즘 알아보기